1. There is no atmosphere on the surface of moon while there is atmosphere on the surface of earth – why?

This happens because of the lower value of escape velocity on the surface of moon compared to that on the surface of earth.

The escape velocity, is given by

   

where is the acceleration due to gravity and is the radius of the planet (or, moon). Taking the standard values of different quantities we can compare the escape velocities on earth () and on moon ()

   

or,

   

Since the escape velocity on the surface of moon is much smaller than the corresponding value on earth’s surface, the atmospheric particles could gradually leave the environment of moon.

2. Does the escape velocity of a particle from a planet depend on its mass?

No.

A prticle can escape from the planet if its kinetic energy is enough to do the work required to move the body from the surface of the planet to infinite distance. This work done () is same as the change in potential energy of the body when it is on the surface and when it is at infinite distance and is given by

   

Here G, M, m, and R are, respectively, the universal gravitational constant, mass of the planet, mass of the body, and the radius of the planet.

Thus we have

   

or,

   

Therefore it is clear that the escape velocity depends on the mass and radius of the planet and not on the mass of the particle.

3. Two satellites revolve around the earth at the same altitude. One of them is ten times the other in mass. Which one is moving faster?

They have the same speed.

Here, we need to check for the expression for the speed of the satellite. For a satellite the force of gravity supplies the required centripetal force. So, we have

   

or,

   

Here and are the mass and altitude of the satellite.

So, we can see that the speed of the satellite does not depend on , the mass of the satellite.

4. A boat loaded with stones floats in a pond. If the stones are dropped into the water what will happen to the level of water?

The water level falls.

Let , and are, respectively, the densities of the stone and water and be the volume of the stone. Here, we will compare the levels of water when the stone is in the boat (level-1) and when the stone is inside water (level-2) with the level when the stone is neither in the boat nor inside water (level-0).

The rise from level-0 to level-1 is due to the displacement of water that creates an upthrust to balance the weight of the stone, so that

   

or,

   

Here, is volume of displaced water in this case.

On the other hand the rise from level-0 to level-2 is due to the displacement of water, directly, by the stone. So,

   

Here, is the volume of water displaced when the stone is in water.

Clearly, as (as stone is denser than water). Therefore level-1 is higher than level-2 and it can be concluded that the level of water falls (from level-1 to level-2) when the stone is placed in water from the boat.

5. A container, partially filled with water, is placed on a weighing machine. A piece of iron is now kept fully immersed inside the water of the container by keeping it suspended with the help of a thread. The iron-piece does not touch any portion of the container and no water spills over. Will there be any change in the reading of the weighing machine? – Explain.

The reading of the weighing machine will increase.

When the piece (iron) is immersed in the water it experiences an upthrust and the person carrying it feels a decrease in its weight. This upthrust is applied by water on the iron-piece. According to Newton’s 3rd law (of motion) – equal and opposite (downward) force would act on water. This force finally acts on the base of the container resulting in an increase in the reading of the weighing machine.

6. A spring of force constant 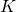is cut into three equal pieces. What is the force constant of each piece?

The force constant of each piece is .

If force elongates the spring by an amount then we have . This implies that by the same force () each piece has been elongated by an amount . Therefore, for each piece we have, , where is the force constant of each part. Comparing the two expressions for we have or .

7. Three springs, each of force constant 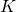, are joined in series. What is the force constant of this combination?

The force constant of the combination is .

If force elongates each spring by an amount then we have . When joined in series, force elongates each one by . Thus the total elongation of the combined spring is and for the combination, we can have . Comparing the two expressions for we have or .

8. Three springs, each of force constant 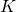, are joined in parallel. What is the force constant of this combination? 

The force constant of each piece is .

If force elongates a spring by an amount then we have . When joined in parallel the force is equally shared by three springs and each spring experiences a force producing an elongation of in each of them. As they are in parallel the elongation of the system is also .  This implies that the same force () elongates the system by an amount . Therefore, for the combined system, we have, , where is the force constant of the combined system. Comparing the two expressions for we have or .

9. A hollow spherical metal ball is filled with water and used as a pendulum. As it starts oscillating water starts to come out through a small hole at its lower end. Will it affect the period of oscillation? If yes, – how?

Yes, the time period () of oscillation will change with time.

We know, for a pendulum , where is the effective length of the pendulum. At first the center of gravity of the ball remains at the center of the sphere. After a while some amount of water leaves the sphere and the center of gravity moves to a lower position which increases resulting in an increase in time period . This continues up to a certain time and after that the amount of water becomes very small and the center of gravity start to go back toward its original position and completely returns there when it is empty. So, we observe an increase and then a decrease in the value of to its original value.

10. An airplane is flying to a city due west from its current location. If there is a slight wind blowing to the southwest, in what direction must the plane head (that is, in what direction must it point)? Explain your answer using a diagram.

The plane must head in a direction making a small angle toward north from west.   

The net velocity of the plane is the sum of the wind velocity and the velocity of the plane in absence of any wind. The wind blow in the southwest direction can be thought of as a combination of its two components – one along west, which is the desired direction and doesn’t deviate the plane from its path, and the other along south and deviates the plane southward. To balance this southward component, the plane should have a northward component in its velocity. Therefore, the plane should have a strong westward and a small northward components.

11. Discuss how relative velocity is related to the direction in which rockets are launched to send them into space. Explain the benefits of using a specific direction for launching rockets. 

All velocities are relative. At the time of launching rockets (carrying the satellite) we need to consider the motion of earth. All the satellite-orbits are relative to the center of mass of the corresponding planets. It should be remembered that before the launching, a satellite already has a motion. Along with earth, the satellite also rotates from west to east. This motion contributes to the tangential speed around the center of mass of earth. This inherent tangential speed is to be considered to calculate the net velocity of the satellite.

As the earth rotates from west to east, the satellite (and the rocket that carries it) has an eastward motion at the time of launching. The existence of this nonzero value of the eastward speed gives an advantage. The rocket is always launched toward east and thus it gains the speed from the earth’s motion, which is about 1675 km/hr (1040 mph), at the equator. This gain in velocity reduces the consumption of fuel, which saves the cost for the launching as well as it has some environmental benefits.

12.Describe three ways that understanding projectile motion and relative velocity could help you improve your success in a basketball game.

1. Understanding projectile motion helps in deciding the speed and angle with which the ball is to be thrown so that the ball can reach the basket or any teammate. That means the knowledge of projectile motion helps in shooting the ball accurately (while throwing from stationary condition).
2. If a player wants to throw the ball to a maximum distance the angle of projection must be 45° above the horizontal. This knowledge from the projectile motion helps in throwing the ball to the biggest possible distance by any particular player.
3. Only understanding the projectile motion would be enough if a player can always throw the ball when she is stationary. But in actual situation, most of the time the player projects the ball while she is in motion. So, at the time of projecting the ball, the existence of the speed (coming from the motion of the player) should be taken into account to shoot the ball accurately.

13. Suggest some situations in which the weight of a body would be zero. 

The weight of a body would be zero if (i) it is taken to the center of the earth (ii) it is falling freely under gravitational force (iii) it is in a orbiting satellite.